UNA FUNCIÓN TRIGONOMÉTRICA ES AQUELLA QUE ESTA ASOCIADA A UNA RAZÓN TRIGONOMÉTRICA. ESTAS EXTIENDEN SU DOMINIO A LOS NUMERO REALES.
LAS RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO a SON LAS OBTENIDAS ENTRE LOS TRES LADOS DE UN TRIÁNGULO RECTÁNGULO. ES DECIR, LAS COMPARACIONES POR SU COCIENTE DE SUS TRES COSTADOS a, b Y c.
EXISTEN 6 FUNCIONES TRIGONOMÉTRICAS:
SENO: EL SENO DE UN ÁNGULO a SE DEFINE COMO LA RAZÓN ENTRE EL CATETO OPUESTO Y LA HIPOTENUSA.
GRÁFICA:
PROPIEDADES:
| Dominio | (todos los números reales) R |
| Recorrido o Imagen |  |
| Continuidad | Es continua en todos los puntos |
| Simetría | Simetría impar |
| Periodicidad | Periódica con periodo T = 2p (360º) |
| Puntos de corte con eje Y | En y = 0 |
| Puntos de corte con eje X | En x = kp, (siendo k un número entero) |
| Signo de la función | Positiva en (0º, 180º) (con periodicidad 2p) Negativa en (180º, 360º) (con periodicidad 2p) |
| Máximos | En x = 90º + 2kp, (siendo k un número entero) |
| Mínimos | En x = 270º + 2kp, (siendo k un número entero) |
| Crecimiento | (0º, 90º) U (270º, 360º) (con periodicidad 2p) |
| Decrecimiento | (90º, 270º) (con periodicidad 2p) |
| Tendencia | Si  , no podemos saber a qué tiende "y" |
| Crecimiento | Si  , no podemos saber a qué tiende "y" |
COSENO: EL COSENO DE UN ÁNGULO a SE DEFINE COMO LA RAZÓN ENTRE EL CATETO CONTINUO Y LA HIPOTENUSA.
GRÁFICA:
PROPIEDADES:
| Dominio | (todos los números reales) R |
| Recorrido o Imagen | |
| Continuidad | Es continua en todos los puntos |
| Simetría | Simetría par |
| Periodicidad | Periódica con periodo T = 2p (360º) |
| Puntos de corte con eje Y | En y=1 |
| Puntos de corte con eje X | En x = 90º + kp, (siendo k un número entero) |
| Signo de la función | Positiva en (0º, 90º) U (270º, 360º) (con T= 2p)Negativa en (90º, 360º) (con periodo T= 2p) |
| Máximos | En x = 0º + 2kp, (siendo k un número entero) |
| Mínimos | En x = 180º + 2kp, (siendo k un número entero) |
| Crecimiento | (180º, 360º) (con periodicidad 2p) |
| Decrecimiento | (0º, 180º) (con periodicidad 2p) |
| Tendencia | Si , no podemos saber a qué tiende "y" |
| Crecimiento | Si , no podemos saber a qué tiende "y" |
TANGENTE: LA TANGENTE DE UN ÁNGULO a ES LA RAZÓN ENTRE EL CATETO OPUESTO Y EL CATETO CONTINUO.
GRÁFICA:
PROPIEDADES:
| Dominio | -  R |
| Recorrido o Imagen | R |
| Continuidad | Discontinua en los puntos |
| Simetría | Simetría impar |
| Periodicidad | Periódica con periodo T = p (180º) |
| Puntos de corte con eje Y | En y = 0 |
| Puntos de corte con eje X | En x = kp, (siendo k un número entero) |
| Signo de la función | Positiva en el intervalo (0º,90º) (con periodicidad p) Negativa en el intervalo (90º, 180º) (con periodicidad p) |
| Máximos relativos | No presenta |
| Mínimos relativos | No presenta |
| Crecimiento | (0º, 90º) U (90º, 180º) ( con periodicidad p) |
| Decrecimiento | Nunca decrece |
| Tendencia | Si , no podemos saber a qué tiende "y" |
| Crecimiento | Si , no podemos saber a qué tiende "y" |
COTANGENTE: LA COTANGENTE DE UN ÁNGULO a DE UN TRIÁNGULO RECTÁNGULO SE DEFINE COMO LA RAZÓN ENTRE EL CATETO CONTINUO Y EL CATETO OPUESTO.
GRÁFICA:
PROPIEDADES:
SECANTE: LA SECANTE DE UN ÁNGULO a DE UN TRIÁNGULO RECTÁNGULO SE DEFINE COMO LA RAZÓN ENTRE LA HIPOTENUSA Y EL CATETO CONTINUO.
GRÁFICA:
PROPIEDADES:
COSECANTE: LA COSECANTE DEL ÁNGULO a DE UN TRIÁNGULO RECTÁNGULO SE DEFINE COMO LA RAZÓN ENTRE LA HIPOTENUSA Y EL CATETO OPUESTO.
GRÁFICA:
PROPIEDADES:
FUNCIONES TRIGONOMÉTRICAS DE ÁNGULOS NOTABLES
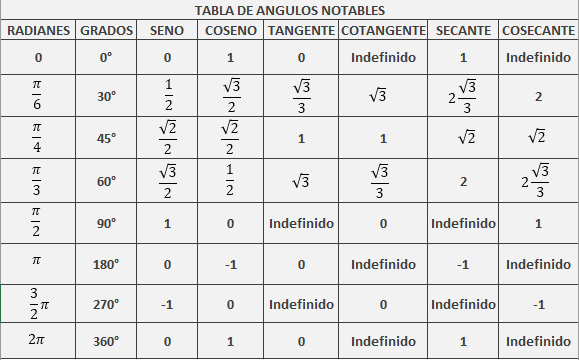
REPRESENTACIÓN GRÁFICA
No hay comentarios.:
Publicar un comentario